Divestadística.es. Eligiendo el método de muestreo más apropiado.

Eulalia Amparo Ruiz Baena
Licenciada en Ciencias y Técnicas Estadísticas
Ayuntamiento de Sevilla
ruizbaena@gmail.com

Diego Daniel Iglesias Espinosa
Licenciado en Ciencias y Técnicas Estadísticas
Instituto de Estadística y Cartografía de Andalucía
diglesias.espinosa@gmail.com

Estudiar toda una población puede ser inviable por su coste en tiempo y recursos. El muestreo permite escoger unos pocos elementos de la población a partir de los que obtener conclusiones para el total. Para que esto sea posible la muestra debe ser representativa.

La representatividad será mayor conforme incremente el tamaño de la muestra, aunque normalmente aumentará el coste. Para conseguir una buena representatividad sin aumentar el coste será necesario mejorar el método de muestreo.

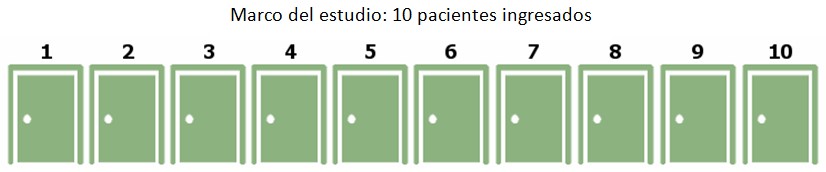
Vamos a ponernos en la piel de un investigador que quiere estudiar las características de los pacientes que han tenido un infarto de miocardio. Hay 10 pacientes ingresados por esta causa pero solo tiene recursos para estudiar en profundidad a 5.

En este pasillo, las habitaciones pares están ocupadas por hombres y las impares por mujeres. Además, los pacientes más graves están alojados en las habitaciones con numeración más alta.

Si los elegimos subjetivamente, según nuestra opinión y experiencia, estaríamos haciendo un muestreo opinático o intencional. La falta de objetividad impediría calcular la probabilidad de selección de cada paciente y el error cometido cuando se extrapolen los resultados de la muestra al conjunto de la población.

El método de muestreo al azar más sencillo es el muestreo aleatorio simple. Todos los pacientes tienen la misma probabilidad de ser seleccionados.

Sin embargo, puede que para nuestro caso no sea el método más apropiado. Si los pacientes más graves están en las habitaciones con numeración más alta, puede ocurrir que se queden fuera o poco representados los de uno u otro extremo.

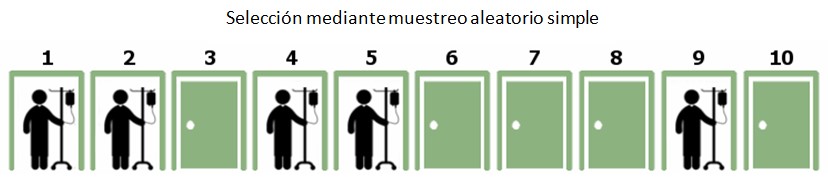
Podemos forzar que esto no ocurra decidiéndonos por un muestreo sistemático, donde se elige un elemento al azar y a partir de él se escogen los demás haciendo un salto constante. Digamos que al azar sale el paciente de la habitación 6. Como tenemos que seleccionar 5 pacientes de un total de 10, elegimos el resto de pacientes con un salto de 10/5=2 posiciones.

¡Oh, oh! Se nos ha pasado un detalle importante: las habitaciones pares están ocupadas por hombres y las impares por mujeres. El muestreo sistemático nos ha llevado a elegir únicamente las habitaciones ocupadas por hombres. Si la enfermedad presenta diferencias por sexos, no podemos escoger sólo hombres o sólo mujeres.

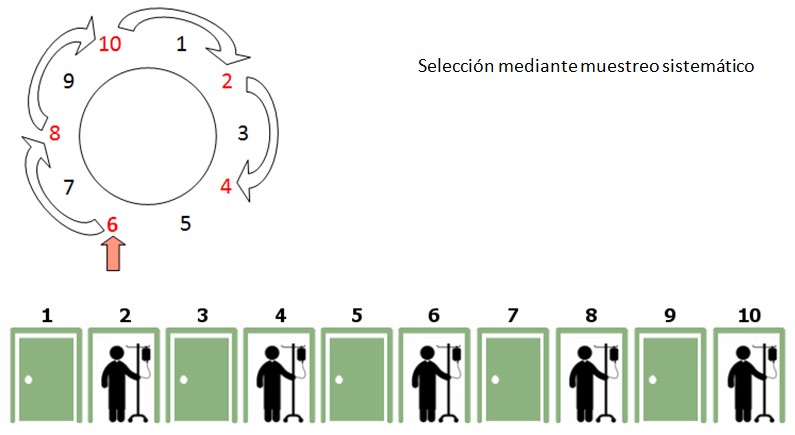
Para solventar este problema vamos a usar un muestreo estratificado. Consiste en dividir la población en grupos de individuos con una misma característica para escoger los sujetos al azar dentro de cada grupo. La división será hombres y mujeres. Seleccionamos al azar 2 hombres y 3 mujeres, porque tenemos un número impar de tamaño de muestra y hemos sorteado qué grupo tendrá más sujetos.

La idea era buena, pero de nuevo nos puede salir toda la muestra en un extremo, en este caso en el extremo inferior.

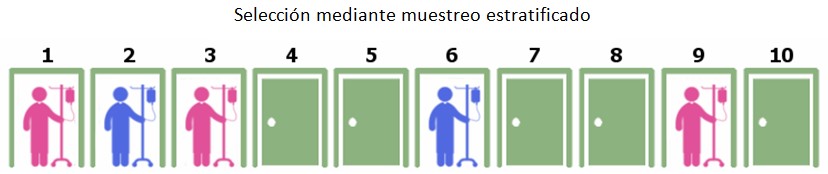
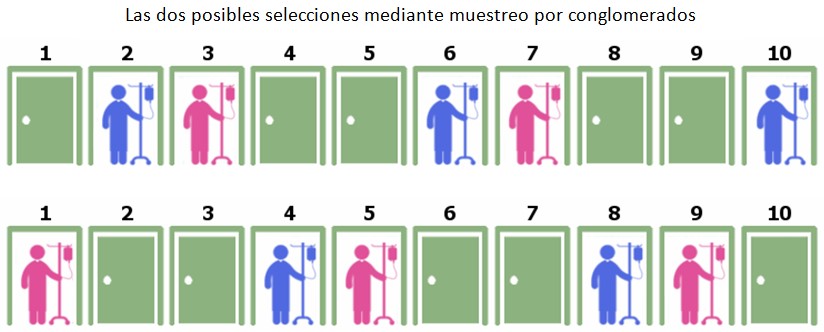
Todavía nos quedan más recursos. Probemos con el muestreo por conglomerados, que divide a la población total en grupos de por sí representativos. Dividimos las 10 habitaciones en 2 grupos de 5 sujetos: Uno formado por 2 hombres y 3 mujeres y el otro por 3 hombres y 2 mujeres, lo más repartidos posible a lo largo del pasillo. A continuación se escoge al azar uno de los dos grupos completos.

Parece que por fin hemos dado con el tipo de muestreo óptimo para nuestro estudio. Hay muchos más tipos de diferente complejidad. Conviene tomarse un tiempo de planificación previo a cualquier investigación porque los resultados ganarán mucho en representatividad.

     Octubre de 2015